音階の数学
皆さま、こんにちは。
IDAJのiconCFD技術サポート担当 Titan0です。
“音階”ってご存知でしょうか?!音楽の時間に、バッハやモーツァルトの絵の前で学んだアレです。(音楽室に貼ってあった著名な音楽家の絵って、なぜ、あんなに怖かったんでしょうか・・・)
音階とは低い音から高い音までを順番にならべて整理したもので、みなさんもよくご存じの“ドレミファソラシド”です。A~Gの音名で表示されることもあります。
ド(C)、レ(D)、ミ(E)、ファ(F)、ソ(G)、ラ(A)、シ(B)
さて話を始める前に、私事ですが、趣味でエレキベースを弾いております。高校時代、女の子の気を引くために楽器を始めようと思い立ち、選んだのがベースでした。あれから20年以上になりますが、腕はたいしたことありません。無念です。
先日、弦をはずしてベース本体を清掃していた時、ふと、各フレット(※1)の位置(=ブリッジ(※2)からの距離)がどのように決められているのか、とても気になりました。
(※1)ボディ側で弦を固定している部位
(※2)ベースやギターの指板上の区切り

調べてみると、ベースやギターなど指板にフレットがある弦楽器は“平均律”という音階となるように配置されているんだそうです。
“平均律”とはなんぞや・・・?ということで音階のお話の始まりです。
“平均律”が誕生するまでには、
ピタゴラス音律 → 純正律 → ミーントーン → ウェル・テンペラメント → 平均律
という過程を経て発達してきました。ここではピタゴラス音律、純正律、平均律についてご紹介します。
ピタゴラス音律(自然音階、ピタゴラス音階)
私たちが良く知っているドレミファソラシは西洋の音階。
そして、この西洋音階を最初に考えたのは、あの「三平方の定理」で有名な、
ピタゴラスさん ↓↓↓

音は数で表現できる!と考え、音程を数の比で表現したピタゴラス音律(ピタゴラス音階)を作りました。
余談ですが、中世ヨーロッパの大学には7自由学科と呼ばれる基礎学問があり、3科目が文化系、4科目が理科系でしたが、なんとその理科系の1つが音楽!!
ピタゴラスさんが活躍した紀元前から始まった音楽に関する研究は、その後も数学・物理学の1つとして研究されていたそうです。
ピタゴラスさんはモノコードと呼ばれる1本だけ弦を張った楽器のようなものを2つ用意し、片方を基準としてもう一方の弦長を変え、それらを同時に弾くという実験を行いました。
これにより弦長の比=2:1、3:2、4:3とすると、2つの音がとても美しく調和することを発見しました。これらをそれぞれ完全8度、完全5度、完全4度と呼びます。
ドレミファソラシドに当てはめると以下の通りです。
2:1 (完全8度) 低いド(C)と高いド(C)の1オクターブ
3:2 (完全5度) ド(C)とソ(G)
4:3 (完全4度) ド(C)とファ(F)
特徴的なのは低いド(C)の弦長を1/2倍すると1オクターブ上のド(C)になります。
これを元に「完全五度の音程にある音を得る」ことを繰り返すことで12半音が決められました。
ではピタゴラス音律でドレミファソラシを奏でるための弦長を計算してみましょう。基本の考え方は以下です。
・完全5度上げると弦長は2/3倍
・1オクターブ下げると弦長は2倍
例えばC(ド)の弦長を1とします。するとドレミファソラシドの弦長は・・・

ん?・・・1オクターブ上のド(C)の弦長が1/2になりませんね。
このようにピタゴラス音律では、基準の音から2倍、2/3倍といった具合に音(=弦長)を決めていくわけですが、オクターブ関係にある音が微妙にズレています。せめてドレミファソラシだけでも意図した音にしたいという場合は、ラ♭(A♭)を基準にします。
ラ♭→ミ♭→シ♭→ファ→ド→ソ→レ→ラ→ミ→シ→ファ#→ド#→ソ#
これでも、結局は同じ音のはずのラ♭とソ#が一致しません。レ#とミ♭も同様です。このズレをピタゴラスコンマと呼びますが、その差約23.5セント(※3)です。
(※3) 23.5セント=半音の約1/4、セントは周波数比を表す単位、平均律の半音=100セント
純正律
ピタゴラス音律では、ドとミといった3度の音は調和しません。同時に鳴らすと音が揺れているように聴こえます。この3度の音も調和させたい!!ということで生まれたのが純正律。
ド(C)の弦長の4/5倍をミ(E)
ファ(F)の弦長の4/5倍をラ(A)
ソ(G)の弦長の4/5倍をシ(B)
と定義します。
これはピタゴラス音律に比べてミ(E)、ラ(A)、シ(B)の音を少し下げていることになります。これによって3度の音も調和するようになりました。しかし、純正律はピタゴラス音律に少し手を加えた音階のため、やはりピタゴラスコンマの問題が残ります。
平均律
もっと使いやすく、もっと自由な音階を!!ということで生まれたのが平均律。
平均律は基準音に対する周波数比の列が等比数列になり、基準音に対するi番目の半音の周波数比fiは以下で計算することができます。
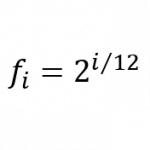
ド(C)を基準とした場合の周波数比fiはこちら。

また1本の弦に着目すると、弦長の比Liは上記周波数比fiの逆数となります。
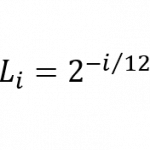
つまり平均律では、各半音の周波数は2の12乗根≒1.06倍で大きくなり、各半音の弦長は2の12乗根の逆数≒0.943874倍で短くなります。
今回のお話のキッカケになった各フレットとブリッジの距離Ln[mm]は、弦長の比Liに開放弦(※4)の長さL[mm]をかけることで得られます。
(※4) 開放弦とは、指板上で弦を全く押さえていない状態のこと
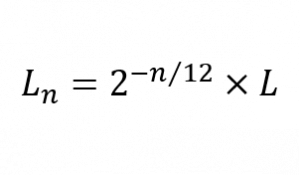
このようにフレット位置が決定された弦楽器には以下の特徴があります。
・1本の弦を開放弦から1フレット→2フレット→3フレットと押さえるところを1つずつボディに近づけていくと半音ずつ上がっていく
・12フレットを押さえると1オクターブ上の音になる
・12フレットの位置で弦長が開放弦の半分になる
平均律はピタゴラス音律と違って、オクターブ関係にある音がズレるということはありません。したがって、転調などがしやすく、現代の音楽で広く利用されている音階です。
しかし、逆に言えばフレットがある弦楽器では平均律でしか演奏ができませんので、もっと和音をきれいに響かせた音楽を!!といった要望にはお応えできそうにありません。
一方で、バイオリンやウッドベース、フレットレスベースなどといったフレットの無い弦楽器では奏者の意図した音階で演奏することができます。
こうなるとどの音階が良いのか?という疑問が出てきそうですが、奏者も聴衆もみんなが心地良い音階で演奏するのがベストですよね、きっと。

今回焦点を当てた音は、上記のような音楽に用いられる「楽音」、つまり聞いていて心地よい音でした。しかし、我々が生活する中では「騒音」に分類される不快な音のほうが多く、この騒音をいかに低減させるかが生活の質を向上させるポイントになります。また騒音が製品の付加価値を左右する要因の一つであるという認識が広がってきており、製品設計において騒音対策は不可欠です。こういった検討を効率的に進めるための有効な手段の1つが音響解析です。
IDAJでは音響解析に関するコンサルティングも実施しております。流体騒音に限らず、広く振動-音響連成問題に対応いたしますので、気になることがありましたら、ぜひ弊社までお問い合わせください。
■IDAJのソーシャルメディア ~ご登録をお願いいたします!~
Twitter:IDAJ@IDAJ_CAE
Twitter:ennovacfd@ennovacfd
Facebook:IDAJ@IDAJ.CAE
Facebook:ennovaCFD@ennovaCFD
Youtube:IDAJ Youtube channel
■IDAJがご提供するオンラインコンテンツをご紹介しています。
■お問合せ先
株式会社 IDAJ 営業部
Webからのお問い合わせはこちら
E-mail:info@idaj.co.jp
