Adjoint法とは？ – その考え方を解説します（1）

2020.08.03 Yutaka Ito

皆さま、こんにちは。

IDAJの伊藤です。

最適設計とは、モノの性能をある目的の状態に近づけるように、形状を創りだしたり、変更することです。今回は、このような最適設計を（矛盾するようではありますが）、なるべく数式を使わずに数理的に定義して考えてみましょう。

「性能」とは、エネルギー損失量、流れから受ける抵抗、熱交換量、強度などといったモノによる、あるいはモノに対する効果のことです。これらの目的の状態に近づける対象となる「性能」を表す定量的な値を、設計の目的になる値という意味で“目的変数”と呼びます。もし、カッコ良さや快適性なども数値として定量的に表すことができれば、これらも目的変数として考えることができます。「性能を目的の状態に近づける」ということは、この目的変数を最小にすることと同義[1]になります。

設計の対象となるモノの形状も、長さ、角度、曲率、あるいはもっと一般的に考えて位置座標というように定量的な値で表して考えます。このような形状を表す定量的な値を“設計変数”と呼びます。

すると、モノの性能は（複数の）設計変数についての関数として考えることができます。

目的関数=f(複数の設計変数)

つまり、形状の最適設計とは、「目的変数を最小化するような設計変数または設計変数の組を見つけること」と定義することができます。

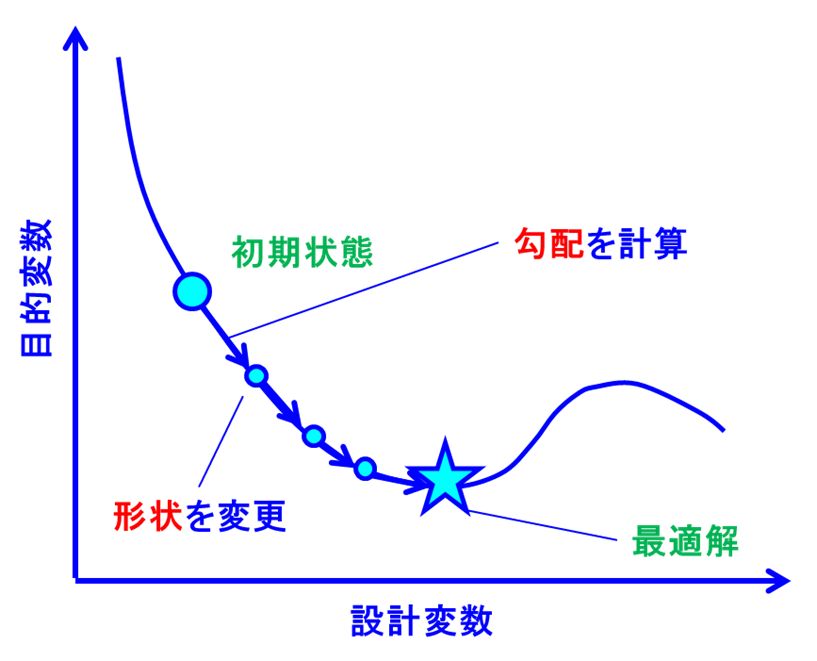
ここで、関数fは目的関数と呼ばれるものです。これの最小値となる設計変数を設計空間の中に見つけるためには、目的関数fの設計変数に対する勾配（微分）がゼロになる点、つまり勾配に対する「解」を見つける必要があります。しかし、一般的に目的関数は設計変数の関数として陽に表せないこともあって、これを直接的に求めることは困難です。そのため、現在の設計変数での目的関数の局所的な勾配を求めて、この勾配の情報から設計変数を少しずつ変化させて、目的関数を小さくする勾配法を使います。

たとえるなら、谷にボールが転がってく様子をイメージして、勾配が負である方向に設計変数を変化させれば良いわけです。

目的関数の勾配を解析的に求めることはやはり難しいため、数値的に求めることになります。この方法として、あるひとつの設計変数を少しだけ変えて、目的変数を再評価し、差分的に勾配を求める差分法という勾配の評価方法があります。この差分法は、直接的で分かりやすい方法なのですが、一度の形状変更のたびに、少なくとも設計変数の数（自由度の数）だけ目的変数を評価する必要があります。このため、特に流体解析や構造解析など計算時間がかかる方法によって目的変数の値を求めなければならない場合には、設計変数の数が増えれば増えるほど、計算コストが大幅に増大します。

これに対してAdjoint法は、設計変数の数に依存せずに勾配を求めることができる手法です。

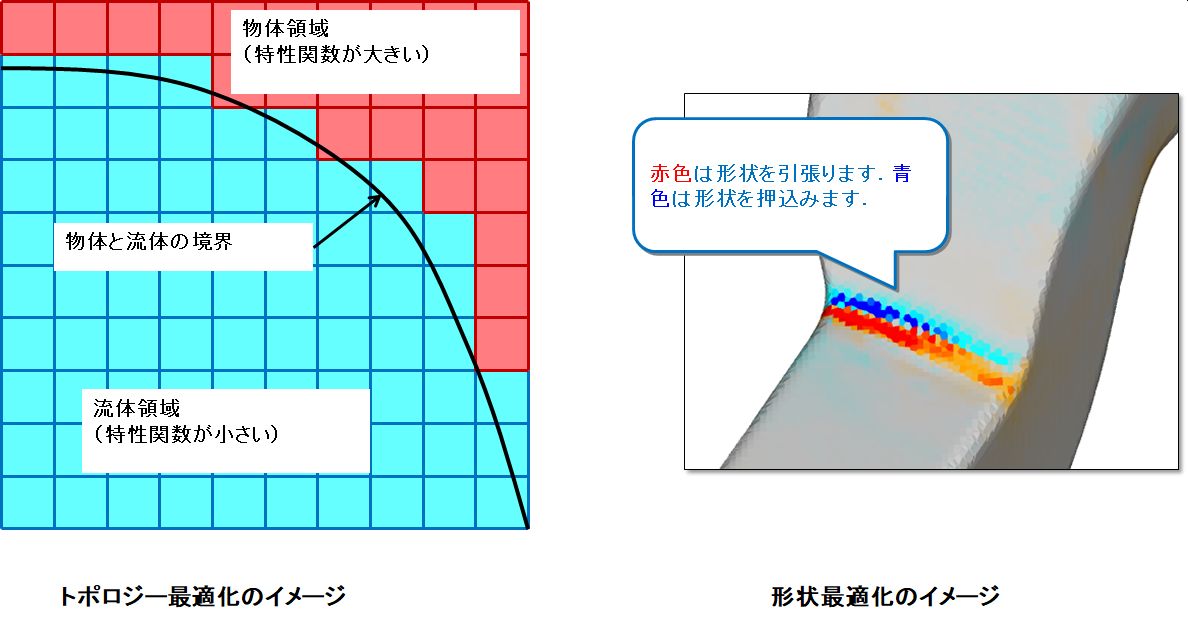
Adjoint法で考える設計変数は、ある点が固体か流体（構造設計の場合は空隙）かを表す特性関数と呼ばれる値、あるいは元の形状からの法線方向の移動量などの場の値としても表すことができます。ちなみに、前者を設計変数とする手法をトポロジー最適化、後者を設計変数とする手法を形状最適化と呼びます。

これらの設計変数は場の値なので、無限個の自由度となります。

このように無限個の自由度がある設計変数でも、1回の計算で勾配を求めることができるのがAdjoint法なのです。次回は、このAdjoint法の考え方についてもう少し詳しくご紹介したいと思います。