Adjoint法とは? – その考え方を解説します(2)
皆さま、こんにちは。
IDAJの伊藤です。
前回に引き続き、最適設計におけるAdjoint法の考え方をご紹介したいと思います。

Adjoint法は、Lagrangeの未定乗数法を応用した方法です。
Lagrangeの未定乗数法は、制約条件を考慮しながら関数の極値を求めるための方法です。制約条件とは、設計変数の取ることのできる範囲を等式で表したものです。不等式の場合もあるのですが、ここでは等式の場合のみを考えます。
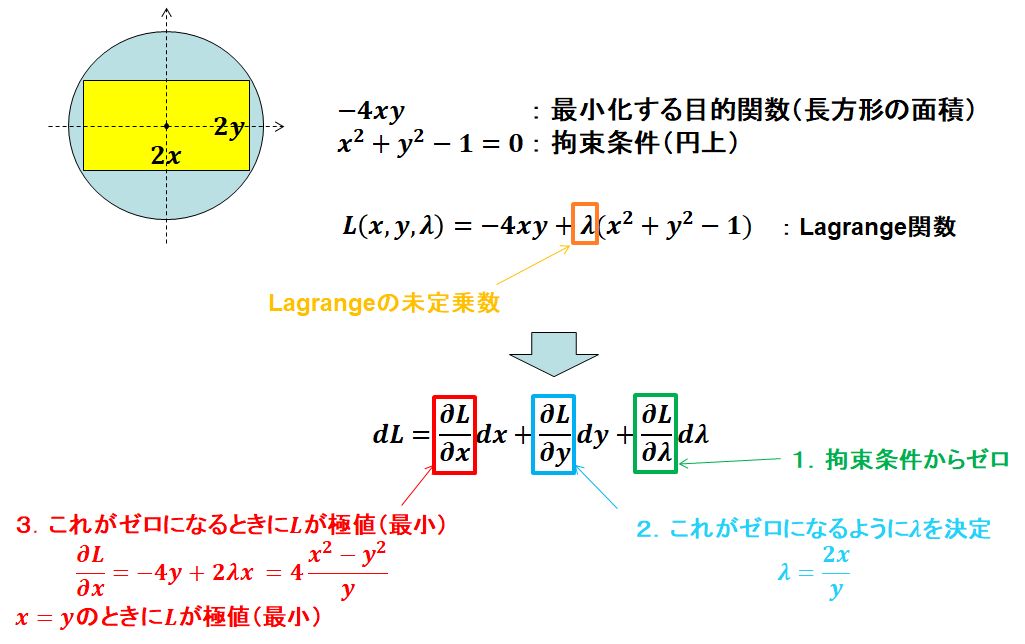
いま、半径1の円に内接する長方形の面積を最大化する問題を考えます。なお、円と長方形の重心は共に原点にあるものとします。このとき、設計変数を長方形の長辺と短辺の長さの半分とし、目的変数は、最小化として定義したいので、長方形の面積に「-1」を掛けた値とします。また、円に内接するという条件から、長辺と短辺の長さはそれぞれ自由に決めることはできず、長方形の頂点が円周上にあるという条件式が満足されなければなりません。この条件式を制約条件と呼び、これを表す関数を制約関数と言います。
制約条件を満足する範囲で、目的変数が極値(最小値)を取るためには、制約関数の勾配ベクトルと目的関数の勾配ベクトルの方向が平行になる必要[1]があります。この条件を式として表したものがLagrange関数とよばれるものです。このときの勾配ベクトルどうしの比例定数をLagrangeの未定乗数と呼びます。Lagrange関数に対する未定乗数と設計変数の微分がゼロになる点が目的変数の極値(最小値)になります。
今考えている最適設計でも、設計変数を決定してから目的変数を評価するのですが、ほとんどの場合、目的変数は設計変数からではなく物理量から求めます。この物理量は形状
(設計変数)を決めたら、物理法則となる基礎方程式と境界条件から決定されるものです。つまり、物理量は自由に値を取ることができるのではなく、物理現象の基礎方程式を満足していなければなりません。これは基礎方程式を、目的関数を最小化する上での制約条件として捉える必要があるということです。
まず、物理現象の基礎方程式それぞれに対してLagrangeの未定乗数に対応するAdjoint変数(随伴変数)を導入します。そしてAdjoint法でのLagrange関数は、基礎方程式それぞれに対してAdjoint変数を乗じて、対象空間内で体積積分をした値を目的関数に加えることで定義します。このように作られたLagrange関数は、設計変数、物理量、Adjoint変数についての汎関数になっていますので、変分法という考え方を使用して勾配を考えることができます。
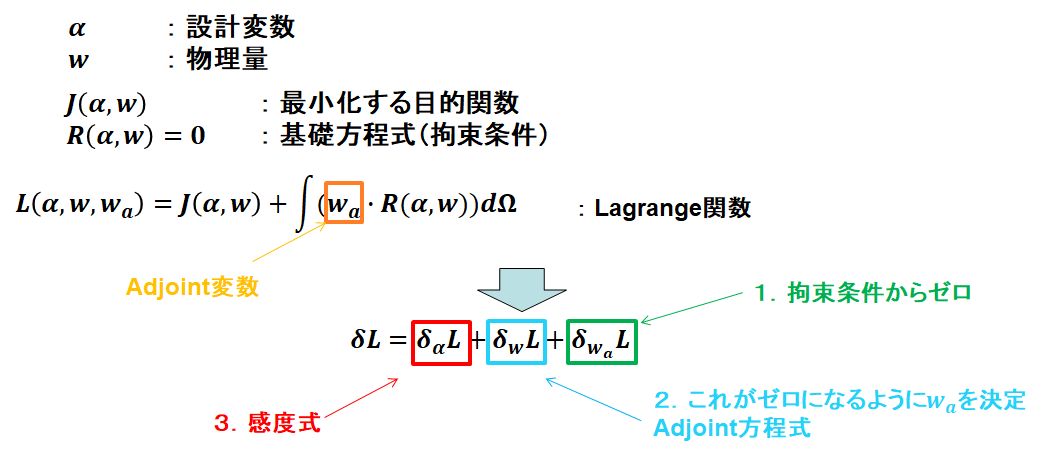
Lagrange関数のAdjoint変数について変分は、基礎方程式そのものになりますので、これが満足されるように各物理量が決定されます。また、各物理変数についての変分をゼロと置いた式をAdjoint方程式と呼び、基礎方程式から求められた物理量と、このAdjoint方程式から各Adjoint変数の空間分布を求めることができます。一般的に、このAdjoint方程式は元の基礎方程式に似た形になっており、計算コストも基礎方程式を解くコストと大きくは変わりません。
これで、変数の値が全て得られましたので、設計変数についての変分を数値的に求めることができます。これがゼロとなったときにLagrange関数が極値(最小値)となり、目的関数も極値(最小値)となりますので、これが、求めたかった“制約条件を満足する空間”での目的関数についての設計変数の勾配です。この式は感度式とも呼ばれます。この感度式に応じて、勾配法の考え方から形状を少しずつ変更していくことで最適形状を求めることができるのです。

[1]制約条件が複数ある場合には、目的関数の勾配ベクトルが、それぞれの制約条件の勾配ベクトルの線形結合で表される必要があります。例えば、設計変数が3つで制約条件が2つの場合を考えます。それぞれの設計変数を座標軸とする3次元空間内の点が設計点になり、制約条件はこの3次元空間内の曲面になります。すると、2つの制約条件を満足する設計点は、曲面と曲面が交わる曲線になり、制約条件を満足する設計点はこの曲線上の点でなければなりません。この曲線上のある設計点で曲線に直交する平面を考えると、制約関数の勾配ベクトル(制約条件を表す曲面の法線ベクトル)は2つともこの平面内にあることになります。もし、この設計点での目的関数の勾配ベクトルがこの平面上になければ、曲線の進む(戻る)方向に成分を持つことになるので、曲線上を設計点が移動すると目的変数の値が変化することになり、そのような設計点は極値ではありません。設計変数が任意の次元の場合でも、これと同様です。
2回にわたって「Adjoint法とは? – その考え方を解説します」というタイトルで記事を書かせていただきました。では、実際にはどのようにして設計開発に適用するのか?!個別のご相談は、以下のお問合せ窓口から承りますで、どうぞお気軽にご相談ください!
追記・更新:2023年4月3日
■IDAJのソーシャルメディア ~ご登録をお願いいたします!~
Twitter:IDAJ@IDAJ_CAE
Twitter:ennovacfd@ennovacfd
Facebook:IDAJ@IDAJ.CAE
Facebook:ennovaCFD@ennovaCFD
Youtube:IDAJ Youtube channel
■IDAJがご提供するオンラインコンテンツをご紹介しています。
■お問合せ先
株式会社 IDAJ 営業部
Webからのお問い合わせはこちら
E-mail:info@idaj.co.jp
