modeFRONTIER多目的ロバスト設計最適化支援ツール
機能2
- 直感的でわかりやすい日本語GUI
- 豊富なダイレクトインターフェースを標準搭載
- 分散実行環境構築が容易
- 実験データを活用した仮想最適化
- 豊富な応答曲面手法
- 一般的な実験計画法から独自手法まで
- 他社の追随を許さない最先端の探索アルゴリズム
- 多目的ロバスト設計による同時満足化
- 50以上の結果処理機能、多変量解析機能
- 設計の原理原則抽出支援機能(CAP)
- 基本モジュール / Runtimeモジュール / Advance / Standard / Basic
※詳細構成はお気軽にお問い合わせください。
一般的な実験計画法から独自手法まで
modeFRONTIERの実験計画法は、直交表や乱数定義など、一般的な手法がほぼ網羅されています。さらに独自の手法として、実際に利用する場面で非常に有効な手法が多数搭載されているのも、modeFRONTIERの大きな特徴のひとつです。
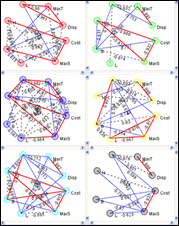
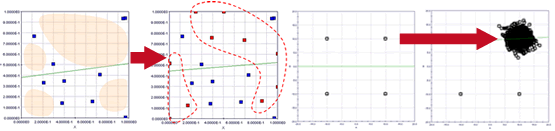
- 入力(設計)値の組み合わせに厳しい拘束条件があった場合、現実的な解探索のためには、あらかじめ「矛盾した組合わせ」を初期の時点から極力排除したい
→「制約充足問題」が有効 - サンプリング領域の疎密を判断し、サンプリング点を加えたい(減らしたい)
→「増補式空間充填法」 、「均等間引き法」が有効 - 応答曲面生成時に近似精度を確保しつつ、できるだけデザインを間引きたい
→「データセット間引き法」が有効
また、一般的によく利用されている直交表も、制御因子、誤差因子それぞれ255因子まで使用でき、さらにオリジナル直交表を組み込むことも可能です。
他社の追随を許さない最先端の探索アルゴリズム
最適化計算をおこなうには、探索アルゴリズムを決める必要があります。
「あれこれ手法を選びたくない。対象に関係なく、効率の良いアルゴリズムは無いか?」
「自動的にアルゴリズムを選べないか?」
これらに対する答えは、“No Free Lunch Theorem”。
つまり、「どんな問題に対しても、平均的に効率良く解けるような探索アルゴリズムは存在しない」という定理(解空間の事前知識無しに、あらゆる目的関数に関して他を常に上回る探索性能を示すアルゴリズムは存在しない、という意)が一般的です。複数の手法の自動切替えやブレンド法が提案されるも、実用上、”万能”と呼ぶのは困難です。
modeFRONTIERは、「現場のニーズにあった手法を搭載する」ということに着眼点を置き、多(単)目的関数対応手法をバランスよく搭載しており、またその搭載数は他社ツールと比較して圧倒的に多いことが特長です。
- とにかく簡単に!複雑な設定はしたくない
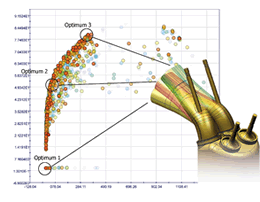
→オートノマス(自律型最適化)によって、最適化の回数もしくは最適化にかけられる計算時間だけを設定して探索 - 探索するための実計算の実行を極力減らし、効率的に最適化したい
→従来の応答曲面併用型最適化アルゴリズムFASTに加え、Hybrid、 ESTECO独自の自律型アルゴリズムpilOPT、など、多彩なアルゴリズムから選択が可能 - とにかく少ない時間でパレート最適解までたどり着きたい
→ゲーム理論を応用したMOGTが有効 - 強拘束・非線形多峰性の多目的最適化問題に取り組みたい
→MOSA、MOGA-II、MOEGOが有効 - 目的関数が多く、通常の多目的最適化アルゴリズムでは非効率
→ESTECO独自に開発した多数目的最適化アルゴリズムMANYが有効 - 応答曲面生成の際、その応答曲面の精度向上のために出力値が急激に変化する場所にサンプリングを自動定義したい
→MACK、リップシッツサンプリングが有効
多目的ロバスト設計による同時満足化
ロバスト性を考慮した設計は、一般的には試作をベースとしたトライ&エラーが主体です。数学的なアプローチとしてもいくつか提唱されていますが、その一般的な方法の前提・課題としては、「変動要因を所定の量だけ変動させて(Δx)、応答の変動を評価すれば良い」という考えがあります。
しかし、現実の問題はそれほど単純ではなく、評価自体が難しいことがあります。また、品質工学では交互作用のある設計は認められておらず、そのため、最近では確率論を用いたアプローチによるロバスト設計での取り組みが注目されています。
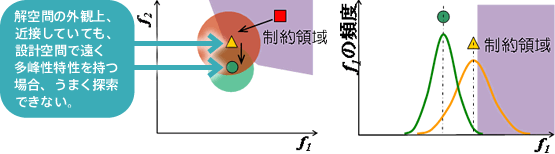
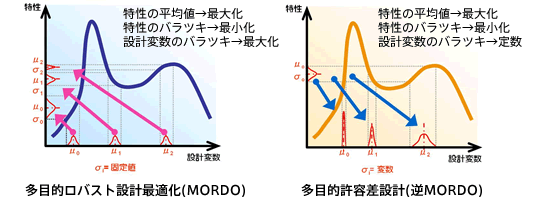
従来までの、一般的な方法の前提・課題
- ロバスト解探索の際、性能最良点(Δ)を起点にするため、ロバスト点(○)が設計空間で近接していることが必要。
- 探索がうまく行かない場合は、重み係数値の試行錯誤が必要。
正方向探索 (入力バラツキ→出力μ、σ):MORDO
「出力の性能重視、かつ出力のロバスト性重視のトレードオフ最適化」などといった、バラツキが存在する設計変数を用いた多目的最適化が可能です。
逆方向探索 (出力μ,σ→入力バラツキ):逆MORDO
「出力のロバスト性を規定値範囲内に抑えつつ、性能を最大化する」ときの設計変数の値と、その許容バラツキ量の組み合わせを、逆算することが可能です。
50以上の結果処理機能、多変量解析機能
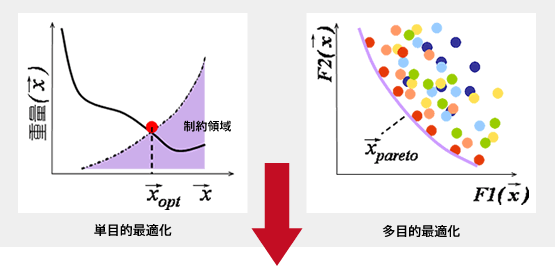
一般の統計分析・最適化ツールでも、豊富な結果処理機能が搭載されています。しかし、数値最適化が求める「解」はあくまで「数値」であり、目的関数を最大化/最小化する入力値の組合わせに過ぎないのも事実です。
最適化手法やツールの発展が複雑な問題の解探索を可能にしましたが、最適になる理由など、物理的意味合いを示すことができたとは未だ言いきれず、最終的には技術者自身による判断が必要です。そのため、自動探索された「最適解」だけではなく、「なぜそれで良いのか」「どうすると悪化するか」といった「最適解になる物理的な理由」を見出すための機能が、本来、最適化ツールには備わっているべきと考えられます。
modeFRONTIERは、その要請にこたえうる、高度なデータマイニング機能が多数搭載されています。
効果量支配率チャート
寄与度の高い変数をリスト表示
相関マトリクス
相関係数値の大きい2変数をランキング表示
マルチベクトルチャート
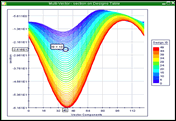
カーソルを波形に置くことで、
デザインIDとカーソル位置の値を表示
散布図マトリクス
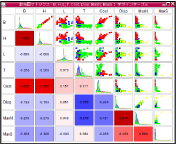
拡大縮小表示により詳細を把握
多次元解析チャート
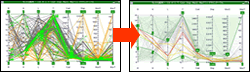
デザイン分布からデザインの特徴を把握
RSM 三次元マップ
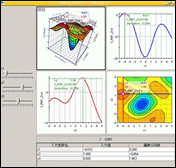
属性値マップチャート
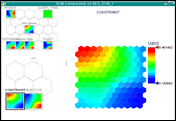
選択した属性値マップでユニットのスクリーニングが可能
設計の原理原則抽出支援機能(CAP)
CAP(Computer Aided Principle)は横浜国立大学大学院 工学研究院 于 強 教授が提唱する、設計原理の抽出を支援する手法です。
設計変数と特性値との関係を明らかにすることにより、「何が最適か」ではなく「なぜ最適か」を抽出することを目的として、設計者に現象を理解するための「ヒント」を与えることに主眼をおいています。(基本特許:特願2006-542362〈EP20050799144〉)
CAP用のチャートによって、各クラスタの特性の平均値をクラスタ散布図で示し、散布図上で望ましい方向へ移動するときに説明変数がどういう傾向で変化するかということを、クラスタ多次元解析チャートで確認できます。 またCAP相関分析チャートでは、1つのクラスタ内部の変数間の相関を確認できます。
デンドログラム
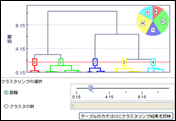
クラスタリングSOM
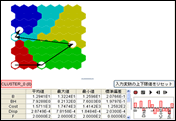
クラスタ散布図
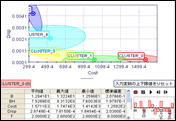
クラスタ多次元解析チャート
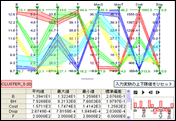
CAP相関分析